SEJARAH BILANGAN

 A. Pengertian Bilangan

 

    Pada mulanya di zaman purbakala banyak bangsa-bangsa yang bermukim sepanjang sungai-sungai besar. Bangsa Mesir sepanjang sungai Nil di Afrika, bangsa Babilonia sepanjang sungai Tigris dan Eufrat, bangsa Hindu sepanjang sungai Indus dan Gangga, bangsa Cina sepanjang sungai Huang Ho dan Yang Tze. Bangsa-bangsa itu memerlukan keterampilan untuk mengendalikan banjir, mengeringkan rawa-rawa, membuat irigasi untuk mengolah tanah sepanjang sungai menjadi daerah pertanian untuk itu diperlukan pengetahuan praktis, yaitu pengetahuan teknik dan matematika bersama-sama. Sejarah menunjukkan bahwa permulaan Matematika berasal dari bangsa yang bermukim sepanjang aliran sungai tersebut. Mereka memerlukan perhitungan, penanggalan yang bisa dipakai sesuai dengan perubahan musim. Diperlukan alat-alat pengukur untuk mengukur persil-persil tanah yang dimiliki. Peningkatan peradaban memerlukan cara menilai kegiatan perdagangan, keuangan dan pemungutan pajak. Untuk keperluan praktis itu diperlukan bilangan-bilangan.

    Bilangan dahulunya di gunakan sebagai simbol untuk menggantikan suatu benda misalnya kerikil, ranting yang masing-masing suku atau bangsa memiliki cara tersendiri untuk menggambarkan bilangan dalam bentuk simbol diantaranya:

 • Simbol bilangan bangsa babilonia.

 • Simbol bilangan bangsa Maya di Amerika pada 500 tahun SM.

 • Simbol bilangan menggunakan huruf  Hieroglif yang dibuat bangsa mesir kuno.

 • Simbol bilangan bangsa Arab yang di buat pada abad ke-11 dan di pakai kini oleh umat islam di seluruh dunia.

 • Simbol bilangan bangsa Yunani Kuno.

 • Simbol bilangan bangsa Romawi yang juga  masih di pakai hingga kini.

        Dalam perkembangan selanjutnya, pada abad ke-X manuskrip Spanyol yang memuat penulisan simbol bilangan oleh bangsa Hindu-Arab Kuno dan cara penulisan inilah yang menjadi cikal bakal penulisan simbol bilangan yang kita pakai hingga saat ini.

 

B. Pengertian Teori Bilangan

    Secara tradisional, teori bilangan adalah cabang dari matematika murni yang mempelajari sifat-sifat bilangan bulat dan mengandung berbagai masalah terbuka yang dapat dipahami meskipun bukan oleh ahli matematika. Dalam teori bilangan dasar, bilangan bulat dipelajari tanpa menggunakan teknik dari bidang matematika lainnya.
    Berikut akan diuraikan perkembangan teori bilangan mulai dari peradaban bangsa Babilonia, bangsa Mesir, bangsa Cina Kuno, bangsa Maya, bangsa Yunani, bangsa Romawi, bangsa India, hingga bangsa Arab (Kusaeri, 2017: 17-36).

• Sistem Bilangan Bangsa Babilonia

        Bangsa Babilonia merupakan bangsa pertama yang menggunakan simbolisasi bilangan. Simbolisasi yang digunakan oleh bangsa Babilonia adalah sistem bilangan basis 60 atau sistem bilangan seksagesimal yang dicampur dengan basis 10. Dari sinilah diturunkannya penggunaan bilangan 60 detik dalam satu menit, 60 menit dalam satu jam, dan 360 derajat dalam putaran lingkaran penuh. Sistem bilangan ini sudah mengenal tempat dan mulai digunakan sekitar tahun 200 SM (Sebelum Masehi), namun masih belum mengenal angka nol. Kemudian sekitar abad ke-2 SM bangsa Babilonia mulai mengenal angka nol yang dilambangkan dengan spasi

• Sistem Bilangan Bangsa Mesir Kuno

 

      Bangsa Mesir Kuno telah mengenal tulisan dan sistem bilangan yang disebut dengan sistem hieroglyph. Sistem bilangan ini menggunakan basis 10 yang telah digunakan sejak 2.850 SM. Sebagaimana sistem bilangan Babilonia yang masih belum mengenal angka nol, sistem bilangan Mesir Kuno juga masih memiliki kekurangan yaitu masalah penempatan dalam penulisan. Masing-masing simbol dapat ditulis secara berulang sesuai yang diinginkan asalkan tidak lebih dari sembilan kali pengulangan. Selain itu, dalam penulisan bilangan juga ditulis dengan leluasa, dapat dimulai dari kiri ke kanan, kanan ke kiri, atas ke bawah, maupun bawah ke atas.

• Sistem Bilangan Bangsa Cina Kuno

      

    Bangsa Cina Kuno menemukan notasi posisional bilangan desimal yang disebut dengan rod numeral atau bilangan batang. Sistem yang dikenal pada tahun 213 SM ini sudah mengenal nilai tempat, namun belum mengenal simbol untuk angka nol. Hampir sama dengan bangsa Babilonia, mereka juga menggunakan spasi atau ruang kosong untuk menyimbolkan angka nol. Bahan yang digunakan sebagai alat dalam perhitungan sistem rod numeral berasal dari batang bambu, batang gading, atau besi.

• Sistem Bilangan Bangsa Maya

    Bangsa Maya mengembangkan sistem numerasi yang merupakan hasil adopsi dari tulisan hieroglyph. Sistem numerasi yang digunakan bangsa ini lebih kompleks karena terdiri dari simbol titik dan garis horizontal. Selain menggunakan sistem numerasi, bangsa Maya juga menggunakan sistem alphabetic dalam peradabannya

• Sistem Bilangan Bangsa Yunani 

       

     Bangsa Yunani merupakan bangsa yang teoritikus dan kritis dalam menggali ilmu pengetahuan. Sekitar tahun 600 SM mereka menggunakan sistem attic yang dikenal sebagai sistem acrophonic. Kemudian mereka mengenal sistem numerasi sebagai hasil adopsi dari bangsa Mesir yang dikembangan menggunakan huruf-huruf alphabetic. Oleh karena itu, sistem numerasi bangsa Yunani sering disebut dengan sistem alphabetic.

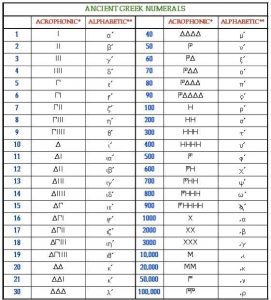
• Sistem Bilangan Bangsa Romawi 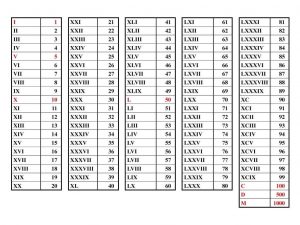       Sistem numerasi bangsa Romawi berkembang pada awal tahun 100 M. Meskipun demikian, awal mula kemunculan sistem bilangan ini belum diketahui secara pasti. Menurut salah satu teori, perkembangan bilangan Romawi didasarkan pada bilangan 5, yaitu V. Kelemahan dari sistem numerasi ini adalah tidak memiliki nilai tempat dan tidak memiliki simbol nol.

• Sistem Bilangan Bangsa India

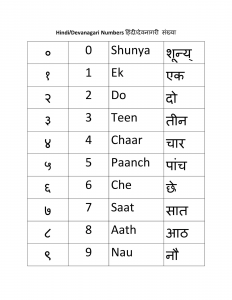
      Sistem numerasi  bangsa India telah digunakan pada tahun 300 SM. Angka yang digunakan pertama kali adalah angka Brahma, kemudian mengalami perubahan menjadi angka Gupta, setelah itu pada tahun 7 SM angka Gupta berkembang menjadi angka Nagari atau Devanagari. Sama seperti bangsa lain, pada awalnya bangsa India juga tidak mengenal simbol nol. Mereka menuliskan angka nol dengan menggunakan tanda kha yang dilambangkan dengan titik atau lingkaran. Tanda ini kemudian mengalami perkembangan, hingga pada tahun 400 M angka nol muncul untuk pertama kali. Pada tahun 628 seorang ahli astronom India Brahma Gupta menulis sistem astronominya yang disebut dengan Siddhanta. Dalam sistem ini, ia menggunakan 9 angka India ditambah dengan angka nol. Sehingga sistem ini telah menjadi sistem bilangan yang lengkap.

• Sistem Bilangan Bangsa Arab

             
      

      Pada abad ke-7 M, sebelum mengenal angka India bangsa Arab menggunakan huruf untuk melambangkan bilangan. Sistem ini disebut dengan al-jumal atau abjad. Kemudian sistem bilangan ini mulai mengalami perkembangan dengan mengadopsi bilangan India ketika masuk ke negara Arab. Sekitar tahun 750 M lambang dan ide nilai suatu tempat sudah dipakai di Baghdad dalam teks bahasa Arab. Ilmuwan Arab yang pertama kali menulis teks berbahasa Latin tentang bilangan India adalah Al-Khawarizmi dengan buku berjudul Algoritma de Numero Indorum. Beliau juga dikenal sebagai penemu angka nol yang digunakan sebagai “Pace Holder” (Penentu Tempat). Pada awal masuknya angka Hindu-Arab ke Eropa menimbulkan pertentangan. Meskipun demikian, angka Hindu-Arab dapat diterima. Sampai pada tahun 1500 M angka Hindu-Arab menjadi sistem bilangan resmi yang dipakai di Eropa.

Kapankah angka nol ditemukan?

      Zero = 0 = Empty = Kosong (Nol) Memang, kata dalam Bahasa Inggris 'zero' (nol) berasal dari bahasa Arab 'sifr', suatu terjemahan literal dari bahasa Sansekerta “shûnya” yang berarti “kosong”. Runtutan keterkaitan bahasa dari masa ke masa: shûnya (Sansekerta) -> (Mesir Kuno/Babilonia) -> (Yunani/Helenik) -> (Roma/Bizantium) – sifr (Arab) -> nol (Inggris) -> nol; kosong (Indonesia) Wikipedia Kata "nol" pada akhirnya berasal dari bahasa Arab "sifr", atau "kosong," terjemahan literal dari bahasa Sansekerta "shûnya". Dengan penggunaan barunya untuk konsep nol, zephyr berarti angin sepoi-sepoi – “hampir tidak ada” (Ifrah 2000; lihat Referensi). Kata zephyr bertahan dengan arti ini dalam bahasa Inggris hari ini. Fibonacci matematikawan Italia (c.1170-1250), yang dibesarkan di Afrika Utara Arab dan dikreditkan dengan memperkenalkan sistem desimal Arab ke Eropa. Sekitar waktu yang sama, matematikawan Arab al-Khawarizmi menggambarkan sistem "bilangan Hindu" dengan notasi posisi dan simbol nol dalam bukunya Kitab al-jabr wa'l muqabalah. Nol asalnya dari India “shûnya” bukan hanya sebuah istilah, tapi juga konsep.

Sekitar tahun 300 SM orang babilonia telah memulai penggunaan dua buah baji miring, //, untuk menunjukkan sebuah tempat kosong, sebuah kolom kosong pada Abakus. Simbol ini memudahkan seseorang untuk menentukan letak sebuah simbol. Angka nol sangat berguna dan merupakan simbol yang menggambarkan sebuah tempat kosong dalam Abakus, sebuah kolom dengan batu-batu yang ditempatkan di dasar. Kegunaannya hanya untuk memastikan bahwa butiran-butiran tersebut berada di tempat yang tepat, angka nol tidak memiliki nilai numerik tersendiri.
Pada komputer nol ini dapat merusak sistem, karena nol diartikan tidak ada. Berapapun bilangan dikalikan dengan nol hasilnya tidak ada. Nah inilah yang membuat bingung dalam operasi perhitungan.
Perhatikan contoh ini :
0=0 ( nol sama dengan nol, benar)
0 x3=0 x 89 (nol sama-sama dikalikan dengan sebuah bilangan, karena juga akan layak nol)
(0 x 3)/0= (0 x 89)/0 (sebuah bilangan dibagi dengan bilangan yang sama, akan layak satu)
3=89 (???, hasil ini yang membuat bingung)
Walaupun sebenarnya nol itu hebat, jika tidak ditemukan angka nol tulisan satu juta dalam bilangan romawi ditulis apa?? Bisa-bisa selembar kertas tidak sampai untuk hanya memberikan simbol satu juta itu. Bisa dibayangkan jika nol tidak ada. Banyak kekuatan yang terkandung dalam angka ini. Nol adalah perangkat paling penting dalam matematika. Namun berkat sifat matematis dan filosofis yang aneh pada angka nol, ia akan berbenturan dengan filsafat barat.
Angka nol berbenturan dengan salah satu prinsip utama filsafat barat, sebuah diktum yang akar-akarnya terhujam dalam filsafat angka Phythagoras dan nilai penting tumbuh dari paradoks Zeno. cosmos Yunani semua didirikan di atas pilar: tak ada liburan.
Kosmos Yunani yang diciptakan oleh Phytagoras, Aristoteles dan Ptolemeus masih lama bertahan setelah keruntuhan peradaban Yunani. Dalam kosmos ini tak ada ketiadaaan. Oleh karena itu, hampir sepanjang dua milinium orang-orang barat tak menerima angka nol. sungguhnya menakutkan. Ketiadaan angka nol menghambat perkembangan matematika, menahan inovasi sains dan yang lebih berbahaya, mengacaukan sistem penanggalan

Macam-macam bilangan

1. Bilangan Bulat adalah bilangan yang terdiri atas bilangan positif, bilangan nol, dan bilangan negatif. Misal : ….-2,-1,0,1,2….
2. Bilangan asli adalah bilangan bulat positif yang dimulai dari angka 1(satu) sampai tak terhingga. Misal : 1,2,3….
3. Bilangan cacah adalah bilangan bulat positif yang diawali dari angka 0 (nol) sampai tak terhingga. Misal : 0,1,2,3,….
4. Bilangan prima adalah bilangan yang tepat memiliki dua faktor yaitu bilangan 1 dan bilangan itu sendiri. Misal : 2,3,5,7,11,13,….(1 bukan bilangan prima, karena memiliki satu faktor saja).
5. Bilangan komposit adalah bilangan yang bukan 0, bukan 1 dan bukan bilangan prima. Misal ; 4,6,8,9,10,12,….
6. Bilangan rasional adalah bilangan yang dinyatakan sebagai suatu pembagian antara dua bilangan bulat (berbentuk bilangan a/b, dimana a dan b merupakan bilangan bulat).  Misal: 1/2 ,2/(3 ),3/4….
7. Bilangan irasional adalah bilangan yang tidak dapat dinyatakan sebagai pembagian dua bilangan bulat. Misal: , 3 , log 7 dan sebagainya.
8. Bilangan riil adalah bilangan yang merupakan penggabungan dari bilangan rasional dan bilangan irasional. Misal: 1/2 (2 ),1/3 5,1/4 ,2/3 log⁡2 dan sebagainya.
9. Bilangan imajiner (bilangan khayal) adalah bilangan yang ditandai dengan i, bilangan imajiner dinyatakan sebagai (-1). Jadi, jika i = (-1) maka i2= -1. Misal: (-4)=⋯? (-4)=√(4×(-1) ) = 4×√(-1) = 2 × i = 2i. Jadi, (-4)=2i.
10. Bilangan kompleks adalah bilangan yang merupakan penggabungan dari bilangan riil dan bilangan imajiner. Misal; (-1)= i. Log (-1)=log⁡i

        SEMOGA BERMANFAAT😊